Travel behavior exploration (off-line)

• ROIs discovery

  • Divide a 2D space into non-overlapping cells

    Because of uncertainty of GPS logs.

  • Determine a set of ROIs

    Calculate the number of trajectories passed with each cell. If it's greater than threshold, it's a ROI.

• ROIs scoring

  • Transform trajecrories

    Transform each trajectory into a sequence of ROIs

• • Construct a user movement graph

    

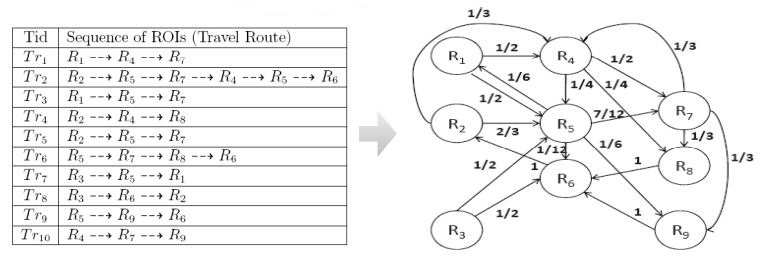
  • Weight of edge < Ri,Rj > is

    $w<R_{i},R_{j}>=\frac{ \sum_{Tr_{h}\in TRD,<R_{i},R_{j}>\subset Tr_{h}} \frac{1}{deg^{+}(R_{i}|Tr_{h})}}{\left | \bigcup_{ R_{l}\in \kappa , R_{i}\neq R_{j}} \left \{ Tr_{k}|Rr_{k}\in TRD, <R_{i},R_{l}> \subset Tr_{k} \right \} \right |}$

    where $deg^+ (R_i|Tr)=|\left \{ R_j|<R_i, R_j> \subset Tr, R_i \neq R_j \right \}|$

  • Attractive scores of ROIs

    Iteratively compute it until scores converge.

    $\begin{pmatrix} S^i(R_1)\\S^i(R_2)\\ \vdots \\S^i(R_m) \end{pmatrix} = M\cdot \begin{pmatrix} 1\\ S^{i-1}(R_1)\\ \vdots\\ S^{i-1}(R_m) \end{pmatrix}$ where

  • $M=\begin{pmatrix} 1-\alpha & \alpha \cdot \omega_{<R_1,R_1> } & \cdots & \alpha \cdot \omega_{<R_m,R_1>}\\ 1-\alpha & \alpha \cdot \omega_{<R_1,R_1> } & \cdots & \alpha \cdot \omega_{<R_m,R_2>}\\ \vdots & & \ddots & \\ 1-\alpha & \alpha \cdot \omega_{<R_1,R_1> } & \cdots & \alpha \cdot \omega_{<R_m,R_2>}\\ \end{pmatrix}$

  • parameter $\alpha = [0,1)$

  • $\omega <R_i,R_j> = 0$

    Use above function to calculate attractive score of each ROI.